The goal of rdecision is to provide methods for
assessing health care interventions using cohort models (decision trees
and semi-Markov models) which can be constructed using only a few lines
of R code. Mechanisms are provided for associating an uncertainty
distribution with each source variable and for ensuring transparency of
the mathematical relationships between variables. The package
terminology follows Briggs et al “Decision Modelling for Health
Economic Evaluation”1.
You can install the released version of rdecision from CRAN with:
install.packages("rdecision")Consider the fictitious and idealized decision problem of choosing between providing two forms of lifestyle advice, offered to people with vascular disease, which reduce the risk of needing an interventional procedure. It is assumed that the interventional procedure is the insertion of a stent, that the current standard of care is the provision of dietary advice, and that the new form of care is enrolment on an exercise programme. To assess the decision problem, we construct a model from the perspective of a healthcare provider, with a time horizon of one year, and assume that the utility of both forms of advice is equal. The model evaluates the incremental benefit of the exercise programme as the incremental number of interventional procedures avoided against the incremental cost of the exercise programme.
The cost to a healthcare provider of the interventional procedure (e.g., inserting a stent) is 5000 GBP; the cost of providing the current form of lifestyle advice, an appointment with a dietician (“diet”), is 50 GBP and the cost of providing an alternative form, attendance at an exercise programme (“exercise”), is 750 GBP. None of the costs are subject to uncertainty, and are modelled as constant model variables.
cost_diet <- ConstModVar$new("Cost of diet programme", "GBP", 50.0)
cost_exercise <- ConstModVar$new("Cost of exercise programme", "GBP", 750.0)
cost_stent <- ConstModVar$new("Cost of stent intervention", "GBP", 5000.0)If an advice programme is successful, there is no need for an interventional procedure. In a small trial of the “diet” programme, 12 out of 68 patients (17.6%) avoided having a procedure, and in a separate small trial of the “exercise” programme 18 out of 58 patients (31.0%) avoided the procedure. It is assumed that the baseline characteristics in the two trials were comparable. The trial results are represented as scalar integers.
s_diet <- 12L
f_diet <- 56L
s_exercise <- 18L
f_exercise <- 40LThe proportions of the two programmes being successful (i.e., avoiding an interventional procedure) are uncertain due to the finite size of each trial and are represented by model variables with uncertainties which follow Beta distributions.
p_diet <- BetaModVar$new(
alpha = s_diet, beta = f_diet, description = "P(diet)", units = ""
)
p_exercise <- BetaModVar$new(
alpha = s_exercise, beta = f_exercise, description = "P(exercise)", units = ""
)The decision tree has one decision node, representing the single choice of the decision problem (i.e., between the two advice programmes), two chance nodes, representing whether each programme is a success or failure, and four leaf nodes (intervention or no intervention for each of the two programmes).
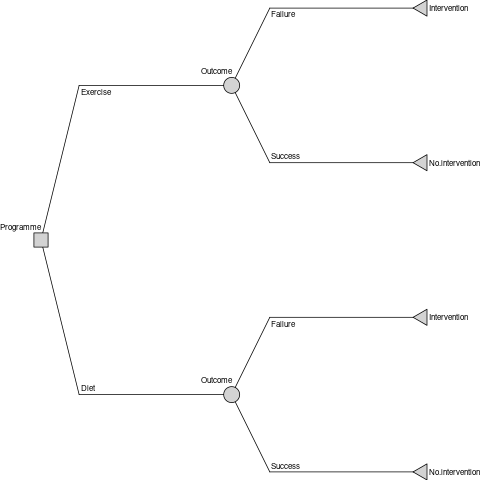
decision_node <- DecisionNode$new("Programme")chance_node_diet <- ChanceNode$new("Outcome")
chance_node_exercise <- ChanceNode$new("Outcome")leaf_node_diet_no_stent <- LeafNode$new("No intervention")
leaf_node_diet_stent <- LeafNode$new("Intervention")
leaf_node_exercise_no_stent <- LeafNode$new("No intervention")
leaf_node_exercise_stent <- LeafNode$new("Intervention")There are two action edges emanating from the decision node, which represent the two choices, each with an associated cost.
action_diet <- Action$new(
decision_node, chance_node_diet, cost = cost_diet, label = "Diet"
)
action_exercise <- Action$new(
decision_node, chance_node_exercise, cost = cost_exercise, label = "Exercise"
)There are four reaction edges, representing the consequences of the
success and failure of each programme. Edges representing success are
associated with the probability of programme success, and those
representing programme failure are assigned a probability of
NA (to ensure that the total probability associated with
each chance node is one) and a failure cost (of fitting a stent).
reaction_diet_success <- Reaction$new(
chance_node_diet, leaf_node_diet_no_stent,
p = p_diet, cost = 0.0, label = "Success"
)
reaction_diet_failure <- Reaction$new(
chance_node_diet, leaf_node_diet_stent,
p = NA_real_, cost = cost_stent, label = "Failure"
)
reaction_exercise_success <- Reaction$new(
chance_node_exercise, leaf_node_exercise_no_stent,
p = p_exercise, cost = 0.0, label = "Success"
)
reaction_exercise_failure <- Reaction$new(
chance_node_exercise, leaf_node_exercise_stent,
p = NA_real_, cost = cost_stent, label = "Failure"
)The decision tree model is constructed from the nodes and edges.
dt <- DecisionTree$new(
V = list(
decision_node,
chance_node_diet,
chance_node_exercise,
leaf_node_diet_no_stent,
leaf_node_diet_stent,
leaf_node_exercise_no_stent,
leaf_node_exercise_stent
),
E = list(
action_diet,
action_exercise,
reaction_diet_success,
reaction_diet_failure,
reaction_exercise_success,
reaction_exercise_failure
)
)
The method evaluate is used to calculate the costs and
utilities associated with the decision problem. By default, it evaluates
it once with all the model variables set to their expected values and
returns a data frame.
rs <- dt$evaluate()Examination of the results of evaluation shows that the expected per-patient net cost of the diet advice programme is 4,168 GBP and the per-patient net cost of the exercise programme is 4,198 GBP; i.e., the net cost of the exercise programme exceeds the diet programme by 31 GBP per patient. The savings associated with the greater efficacy of the exercise programme do not offset the increased cost of delivering it.
Because the probabilities of the success proportions of the two treatments have been represented as model variables with an uncertainty distribution, the uncertainty of the relative effectiveness is estimated by repeated evaluation of the decision tree.
N <- 1000L
rs <- dt$evaluate(setvars = "random", by = "run", N = N)The confidence interval of the net cost difference (net cost of the diet programme minus the net cost of the exercise programme) is estimated from the resulting data frame. From 1000 runs, the mean net cost difference is -18.98 GBP with 95% confidence interval -775.04 GBP to 766.98 GBP, with 47% runs having a lower net cost for the exercise programme. Although the point estimate net cost of the exercise programme exceeds that of the diet programme, due to the uncertainties of the effectiveness of each programme, it can be concluded that there is insufficient evidence that the net costs differ.
The method threshold is used to find the threshold of
one of the model variables at which the cost difference reaches zero. By
univariate threshold analysis, the exercise program will be cost saving
when its cost of delivery is less than 719 GBP or when its success rate
is greater than 31.74%. These thresholds are also subject to
uncertainty.
Sonnenberg and Beck2 introduced an illustrative example of
a semi-Markov process with three states: “Well”, “Disabled” and “Dead”
and one transition between each state, each with a per-cycle
probability. In rdecision such a model is constructed as
follows. Note that transitions from a state to itself must be specified
if allowed, otherwise the state would be a temporary state.
# create states
s.well <- MarkovState$new(name = "Well", utility = 1.0)
s.disabled <- MarkovState$new(name = "Disabled", utility = 0.7)
s.dead <- MarkovState$new(name = "Dead", utility = 0.0)# create transitions leaving rates undefined
E <- list(
Transition$new(s.well, s.well),
Transition$new(s.dead, s.dead),
Transition$new(s.disabled, s.disabled),
Transition$new(s.well, s.disabled),
Transition$new(s.well, s.dead),
Transition$new(s.disabled, s.dead)
)# create the model
M <- SemiMarkovModel$new(V = list(s.well, s.disabled, s.dead), E)# create transition probability matrix
snames <- c("Well", "Disabled", "Dead")
Pt <- matrix(
data = c(0.6, 0.2, 0.2, 0.0, 0.6, 0.4, 0.0, 0.0, 1.0),
nrow = 3L, byrow = TRUE,
dimnames = list(source = snames, target = snames)
)
# set the transition rates from per-cycle probabilities
M$set_probabilities(Pt)
With a starting population of 10,000, the model can be run for 24 years as follows.
# set the starting populations
M$reset(c(Well = 10000.0, Disabled = 0.0, Dead = 0.0))# cycle
MT <- M$cycles(24L, hcc.pop = FALSE, hcc.cost = FALSE, hcc.QALY = FALSE)The output, after rounding, of the cycles function is
the Markov trace, shown below, which replicates Table 22. In
more recent usage, cumulative utility is normally called incremental
utility, and expressed per patient (i.e., divided by 10,000).
| Years | Well | Disabled | Cumulative.Utility |
|---|---|---|---|
| 0 | 10000 | 0 | 0 |
| 1 | 6000 | 2000 | 7400 |
| 2 | 3600 | 2400 | 12680 |
| 3 | 2160 | 2160 | 16352 |
| 23 | 0 | 1 | 23749 |
| 24 | 0 | 0 | 23749 |
In addition to using base R3, redecision
relies on the R6 implementation of classes4 and
the rlang package for error handling and non-standard
evaluation used in expression model variables5. Building the
package vignettes and documentation relies on the testthat
package6, the devtools package7,
rmarkdown10 and
knitr11.
Underpinning graph theory is based on terminology, definitions and algorithms from Gross et al12, the Wikipedia glossary13 and links therein. Topological sorting of graphs is based on Kahn’s algorithm14. Some of the terminology for decision trees was based on the work of Kaminski et al15 and an efficient tree drawing algorithm was based on the work of Walker16. In semi-Markov models, representations are exported in the DOT language17.
Terminology for decision trees and Markov models in health economic evaluation was based on the book by Briggs et al1 and the output format and terminology follows ISPOR recommendations19.
Citations for examples used in vignettes are given in applicable vignette files.